Resultados preicfes
Donald en la tierra de las matemáticas
En esta ocasión el pato Donald es un explorador que viaja
por la tierra de las matemáticas, ahí descubre un río de números, las raíces de
los arboles son cuadradas y animales en forma de figuras geométricas.
Allí conoce al espíritu de las matemáticas quien lo lleva a un fantástico viaje por la tierra de las matemáticas, en donde
aprende mucho sobre ellas, como por ejemplo que encontramos las matemáticas en toda
la naturaleza y en general en todas las
cosas del universo. En este viaje primero lo lleva a la antigua Grecia a
conocer a Pitágoras el padre de las matemáticas y la música; y a los
pitagóricos una sociedad secreta de matemáticos que se dedicaban a buscar y
discutir nuevos descubrimientos, entre los cuales se encontraba la música (gracias
a ellos se plantearon las bases de la música actual).
Pitágoras también descubrió los secretos de la estrella de
cinco puntas, el rectángulo de oro y la sección de oro, los cuales influyeron
mucho en la idea de belleza, esto se puede apreciar en lugares como la catedral
de Notre Dame y también en el arte renacentista como en las pinturas; aun en la
actualidad todavía de usa la idea de belleza de el rectángulo mágico como en
los edificios, pinturas, esculturas y hasta en posturas de baile.
Las figuras geométricas se encuentran muy a menudo en la
naturaleza, y la proporción mágica se encuentra muy a menudo en las formas en
espiral.
Las matemáticas y las figuras geométricas se encuentran también en lo juegos por ejemplo
en el ajedrez se utiliza el calculo matemático, el campo de béisbol es un
diamante, el fútbol americano se juega en un rectángulo, el básquetbol es un
juego de círculos esferas y rectángulos; y en otros juegos como el billar en el
cual se aprende calculo matemático para hacer que la bola llegue donde se desea.
En general la gran mayoría de los descubrimientos científicos del hombre
se han dado gracias a las matemáticas y las figuras geométricas, muchos de
estos descubrimientos abrirán las puertas a muchos otros y así sucesivamente se
convierte en una cadena interminable en donde gracias a ellas podremos labrar
nuestro futuro.
Según las palabras de galileo:-Las matemáticas son el alfabeto con el cual Dios ha escrito el universo.Donald en la tierra de las matemáticas
Donald en la tierra de las matemáticas
GLOSARIO
 PUNTO
PUNTO
En geometría, el punto es uno de
los entes fundamentales, junto con la recta y el plano. Son
considerados conceptos primarios, es decir, que sólo es posible
describirlos en relación con otros elementos similares. Se suelen describir
apoyándose en los postulados característicos, que determinan las
relaciones entre los entes geométricos fundamentales.
El punto es una «figura geométrica» adimensional: no tiene
longitud, área, volumen, ni otro ángulo dimensional. No es un objeto físico.
Describe una posición en el espacio, determinada respecto de un sistema de
coordenadas preestablecido.
SEGMENTO
Es la porción de recta limitada por dos puntos, llamados
extremos.
Se designa por los puntos que lo limitan o por una letra
minúscula.
Tipos de segmentos
Segmento nulo
Un segmento es nulo cuando
sus extremos coinciden.
Segmentos consecutivos
Dos segmentos son consecutivos cuando
tienen un extremo en común.
Segmentos alineados o adyacentes
Dos segmentos
consecutivos están alineados cuando pertenecen a la misma
recta.
RECTA
En geometría euclidiana, la recta o línea recta,
se extiende en una misma dirección, existe en una sola
 Cuando se habla de un plano, se está hablando del objeto
geométrico que no posee volumen, es decir bidimensional, y que posee un número
infinito de rectas y puntos. Sin embargo, cuando el término se utiliza en
plural, se está hablando de aquel material que es elaborado como una
representación gráfica de superficies en diferentes posiciones. Los planos son
especialmente utilizados en ingeniería, arquitectura y diseño ya que sirven
para diagramar en una superficie plana otras superficies que son regularmente
tridimensionales.
Cuando se habla de un plano, se está hablando del objeto
geométrico que no posee volumen, es decir bidimensional, y que posee un número
infinito de rectas y puntos. Sin embargo, cuando el término se utiliza en
plural, se está hablando de aquel material que es elaborado como una
representación gráfica de superficies en diferentes posiciones. Los planos son
especialmente utilizados en ingeniería, arquitectura y diseño ya que sirven
para diagramar en una superficie plana otras superficies que son regularmente
tridimensionales.

Un círculo, en geometría, es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida.
 La circunferencia sólo posee longitud. Se distingue
del círculo en
que éste es el lugar geométrico de los puntos contenidos en una circunferencia
determinada; es decir, la circunferencia es el perímetro del
círculo cuya superficie contiene.
La circunferencia sólo posee longitud. Se distingue
del círculo en
que éste es el lugar geométrico de los puntos contenidos en una circunferencia
determinada; es decir, la circunferencia es el perímetro del
círculo cuya superficie contiene.
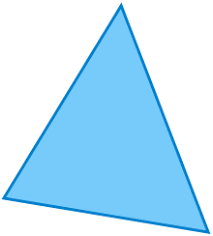 Un triángulo, en geometría,
es un pólígono determinado
por tres rectas que
se cortan dos a dos en tres puntos (que no se encuentran alineados, es
decir: no colineales). Los puntos de intersección de las rectas son los vértices y los segmentos de recta
determinados son los lados del triángulo. Dos lados contiguos forman uno de los
ángulos interiores del triángulo.
Un triángulo, en geometría,
es un pólígono determinado
por tres rectas que
se cortan dos a dos en tres puntos (que no se encuentran alineados, es
decir: no colineales). Los puntos de intersección de las rectas son los vértices y los segmentos de recta
determinados son los lados del triángulo. Dos lados contiguos forman uno de los
ángulos interiores del triángulo.
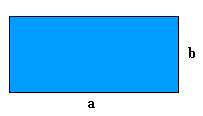 En geometría plana, un rectángulo es un paralelogramo cuyos
cuatro lados forman ángulos rectos entre sí. Los lados opuestos tienen la misma longitud.
El perímetro de
un rectángulo es igual a la suma de todos sus lados.
En geometría plana, un rectángulo es un paralelogramo cuyos
cuatro lados forman ángulos rectos entre sí. Los lados opuestos tienen la misma longitud.
El perímetro de
un rectángulo es igual a la suma de todos sus lados.
 Los ángulos interiores opuestos son iguales. Sus diagonales son perpendiculares entre
si y cada una divide a la otra en partes iguales (esta
característica por sí sola también define al rombo).
Los ángulos interiores opuestos son iguales. Sus diagonales son perpendiculares entre
si y cada una divide a la otra en partes iguales (esta
característica por sí sola también define al rombo).




dimensión y contiene infinitos puntos ; está compuesta de infinitos segmentos (el
fragmento de línea más corto que une dos puntos). También se describe
como la sucesión continua e indefinida de puntos en una sola dimensión, o sea,
no posee principio ni fin.
Semirrecta
Una semirrecta es cada una de las partes en que queda
dividida una recta por uno cualquiera de sus puntos.
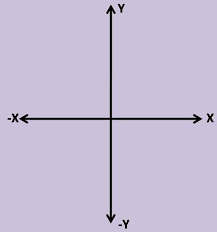
PLANO
SEMIPLANO
Se llama semiplano, en geometría,
a cada una de las dos partes en que un plano queda dividido por
una recta.
CIRCULO
Un círculo, en geometría, es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida.
CIRCUNFERENCIA
Puede ser considerada como una elipse de excentricidad nula, o una
elipse cuyos semiejes son iguales. También se puede describir como la sección,
perpendicular al eje, de una superficie cónica o cilíndrica, o
como un polígono de infinitos lados, cuya apotema coincide
con su radio.
La circunferencia de centro en el origen de coordenadas y
radio 1 se denomina circunferencia unidad o circunferencia goniométrica.
TRIANGULO
Por lo tanto, un triángulo tiene 3 ángulos interiores, 3
ángulos exteriores, 3 lados y 3 vértices.
Si está contenido en una superficie plana se denomina triángulo, o trígono,
un nombre menos común para este tipo de polígonos. Si está contenido en una
superficie esférica se
denomina triángulo esférico. Representado, en cartografía,
sobre la superficie terrestre, se llama triángulo geodésico.
CUADRADO
En geometría euclidiana , un cuadrado es
un paralelogramo que tiene sus cuatro lados iguales y
además sus cuatro ángulos son iguales y rectos tiene 4 ejes de simetría ,4
vértices y 4 aristas.
RECTÁNGULO
El área de un rectángulo es igual al producto de dos de sus
lados contiguos.
ROMBO
El rombo es un cuadrilátero paralelogramo cuyos
cuatro lados son
de igual longitud.
Si un rombo es a la vez un rectángulo,
entonces es un cuadrado. Un rombo con un ángulo interno de 45° suele
llamarse losange.
TRAPECIO
En geometría, se llama trapecio a un cuadrilátero que
tiene dos lados paralelos y otros dos que no lo son. 12 Los
lados paralelos se llaman bases del trapecio y la distancia entre
ellos altura. Se denomina mediana al segmento que
tiene por extremos los puntos medios de los lados no paralelos. Un cuadrilátero
sin lados paralelos recibe el nombre de trapezoide.
Los trapecios respecto a sus ángulos internos, pueden ser
rectángulos, isósceles o escalenos:
Trapecio rectángulo es el que tiene un lado
perpendicular a sus bases.
Tiene dos ángulos internos rectos, uno agudo y otro obtuso.
Trapecio isósceles es el que tiene los lados no
paralelos de igual medida.
Tiene dos ángulos internos agudos y dos obtusos, que son
iguales entre sí.
Las diagonales son congruentes.
El trapecio isósceles es un cuadrilátero cíclico ya que la suma de
los ángulos opuestos es 180°.
Trapecio escaleno es el que no es isósceles ni
rectángulo, la medida de sus lados da medidas diferentes.
Sus cuatro ángulos internos poseen diferentes medidas.
PARALELOGRAMO
Un paralelogramo es un tipo especial de cuadrilátero (un polígono formado
por cuatro lados) cuyos
lados son paralelos dos a dos.Los paralelogramos se clasifican en:
Paralelogramos rectángulos, son aquellos cuyos ángulos
internos son todos ángulos rectos. En esta clasificación se incluyen:
El cuadrado, que tiene todos sus lados de igual longitud.
El rectángulo,
que tiene sus lados opuestos de igual longitud.
Paralelogramos no rectángulos, son aquellos que tienen dos
ángulos internos agudos y dos ángulos internos obtusos. En esta clasificación
se incluyen:
El rombo, que tiene todos sus lados de igual longitud, y dos pares
de ángulos iguales.
El romboide, que tiene los lados opuestos de igual longitud y
dos pares de ángulos iguales.
CUADRILÁTERO
Un cuadrilátero es
un polígono que
tiene cuatro lados. Los
cuadriláteros pueden tener distintas formas, pero todos ellos tienen
cuatro vértices y dos diagonales, y
la suma de sus ángulos internos siempre da como resultado 360º.
Historia de la trigonometría

Los
egipcios establecieron la medida de los ángulos en grados, minutos y
segundos. En el siglo II a.C. Hiparco de Nicea realizo una tabla
trigonométrica con el fin de resolver triángulos, iniciando desde un ángulos de
70° yendo hasta 180° en un incremento de 70°.
A
finales del siglo VIII los astrónomos árabes habían recibido la herencia de las
tradiciones de Grecia y de la India, y prefirieron trabajar con la función
seno.
En
las últimas décadas del siglo X ya habían completado la función seno y las
otras cinco funciones y habían descubierto y demostrado varios teoremas
fundamentales de la trigonometría tanto para triángulos planos como
esféricos. Los árabes calcularon tablas precisas en división sexagesimal.
En
occidente el astrónomo alemán Georges Joachim, introdujo el concepto
moderno de funciones trigonométricas como proporciones en vez de longitudes de
ciertas líneas. François Viète incorporó el triángulo polar en la
trigonometría esférica y encontró fórmulas para expresar las funciones de
ángulos.
En
el siglo XVII Isaac Newton invento el calculo diferencial e integral, sus
fundamentos fue la representación de muchas funciones matemáticas, las cuales
fueron incorporada al análisis donde hoy desempeñan una gran labor en
matemáticas puras como en las aplicadas
En
el siglo XVIII Leonardo fue el que fundo verdaderamente la trigonometría
moderna. Definió las funciones trigonometrías utilizando expresiones con
exponenciales de números complejos. También dio el uso de las letras minúsculas
(a,b,c) en los lados de un triangulo plano esférico, y mayúsculas (A,B,C) en
los lados opuestos.
¿Qué es la Trigonometría y qué estudia?
 La trigonometría (que significa en griego medición de triángulos) es la parte de la matemática, o más específicamente de la geometría, que se ocupa del cálculo de triángulos, comprendiendo sus seis elementos, los tres lados y los tres ángulos. Se parte de al menos tres elementos del mismo, siendo indefectiblemente, uno de ellos, un lado del triángulo. Además tiene por objeto el cálculo en general de todas las figuras que puedan descomponerse en triángulos. Es un conocimiento antiquísimo que se remonta a egipcios y babilonios, desarrollada muy profundamente por los árabes. Tiene amplia aplicación en física,química, ingeniería y astronomía, para medir enormes distancias.
La trigonometría (que significa en griego medición de triángulos) es la parte de la matemática, o más específicamente de la geometría, que se ocupa del cálculo de triángulos, comprendiendo sus seis elementos, los tres lados y los tres ángulos. Se parte de al menos tres elementos del mismo, siendo indefectiblemente, uno de ellos, un lado del triángulo. Además tiene por objeto el cálculo en general de todas las figuras que puedan descomponerse en triángulos. Es un conocimiento antiquísimo que se remonta a egipcios y babilonios, desarrollada muy profundamente por los árabes. Tiene amplia aplicación en física,química, ingeniería y astronomía, para medir enormes distancias.
Usando solo funciones racionales no pueden realizarse cálculos que involucren los seis elementos del triángulo, pues deben relacionarse ángulos medidos en grados, con lados expresados en unidades de longitud.
De acuerdo a los tipos de triángulos de que se ocupa, la trigonometría puede ser plana, cuando se ocupa del cálculo de triángulos de lados rectos (rectilíneos) o esférica, si calcula triángulos esféricos. La goniometría o trigonometría analítica se ocupa de las funciones circulares (seno, tangente y secante, y coseno cotangente y cosecante)
La medida de ángulos más utilizada es el sistema sexagesimal, cuya unidad de medida es el grado, el minuto y el segundo, partiéndose del triángulo recto correspondiente a un cuadrante que tiene 90 grados. Cada grado tiene 60 minutos y cada minuto sesenta segundos. En el sistema centesimal de medición de ángulos, se usan las mismas unidades de medida, pero se considera que un cuadrante tiene 100 grados, cada grado 100 minutos y cada minuto cien segundos.

Suscribirse a:
Comentarios (Atom)
